Ціле завжди складається з частин, частини різної величини знаходяться в певному відношенні один до одного і до цілого.
 Принцип золотого перетину - вищий прояв структурного і функціонального досконалості цілого і його частин у мистецтві, науці, техніці і природі.
 Золотий перетин - гармонійна пропорція
У математиці пропорцією (лат. proportio) називають рівність двох відносин: a: b = c: d.
Відрізок прямої АВ можна розділити на дві частини такими способами:
- на дві рівні частини - АВ: АС = АВ: ВС;
- на дві нерівні частини в будь-якому відношенні (такі частини пропорції не утворюють);
- таким чином, коли АВ: АС = АС: ВС.
Останнє і є золотий розподіл або розподіл відрізка в крайньому і середньому відношенні.
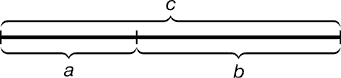
ЗОЛОТИЙ ПЕРЕТИН - це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього.
a: b = b: c або з: b = b: а.
Рис. 1. Геометричне зображення золотої пропорції
Практичне знайомство із золотим перетином починають з розподілу відрізка прямої в золотій пропорції за допомогою циркуля і лінійки.
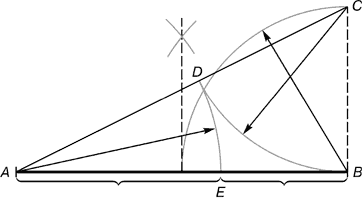
Рис. 2. Розподіл відрізка прямої по золотому перерізу. BC = 1/2 AB; CD = BC
З точки В підіймали перпендикуляр, рівний половині АВ. Отримана точка Зз'єднується лінією з точкою А. На отриманій лінії відкладається відрізок ВС, що закінчується точкою D. Відрізок AD переноситься на пряму АВ. Отримана при цьому точка Е ділить відрізок АВ у співвідношенні золотої пропорції.
Відрізки золотий пропорції виражаються нескінченним ірраціональним дробомAE = 0,618 ..., якщо АВ прийняти за одиницю, ВЕ = 0,382 ... Для практичних цілей часто використовують наближені значення 0,62 і 0,38. Якщо відрізок АВ прийняти за 100 частин, то більша частина відрізка дорівнює 62, а менша - 38 частинам.
Властивості золотого перетину описуються рівнянням:
x 2 - x - 1 = 0.
Рішення цього рівняння:
 Властивості золотого перетину створили навколо цього числа романтичний ореол таємничості і мало не містичного поклоніння.
В Інтернеті є сервіс який автоматично розраховує золоту пропорцію відрізка:
Другий золотий перетин
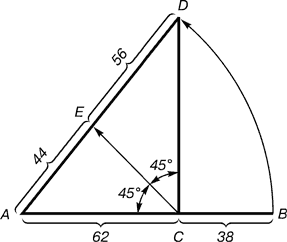
Існує і "другий золотий перетин", яке випливає з основного перетину і дає інше співвідношення 44: 56.
Така пропорція виявлена в архітектурі, а також має місце при побудові композицій зображень подовженого горизонтального формату.
|
| |
Ділення здійснюється наступним чином. ВідрізокАВ ділиться в пропорції золотого перетину. З точкиС, підіймали перпендикулярСD. Радіусом АВ знаходиться точка D, яка з'єднується лінією з точкою А. Прямий кут АСD ділиться навпіл. З точки С проводиться лінія до перетину з лінією AD. ТочкаЕ ділить відрізок AD у відношенні 56: 44.
|
Рис. 3. Побудова другого золотого перетину
Рис. 4. Розподіл прямокутника лінією другого золотого перетину
На малюнку показано положення лінії другого золотого перетину. Вона знаходиться посередині між лінією золотого перетину і середньою лінією прямокутника.
| 
